I think it’s fair to say that most programmers understand type safety as a feature of the programming language which eliminates the type errors. TypeScript as a statically typed superset of JavaScript addresses this issue, especially in the strict mode which is more rigorous and performs additional checks.
That being said, I’m more interested in type safety being understood more as the extent of program correctness rather than just making sure what I expect to be a string is a string and not a number. The goal of this article is to present techniques that you can apply when working on your day-to-day tasks to increase your confidence that your code is correct.
Often in our programs, we have to handle different cases, and the majority of bugs are caused by handling a particular case incorrectly or not handling it at all. This is indeed a very broad definition of what causes bugs, but the remedy is also generic and has many applications. To address issues that originate from incorrectly handling decisions in the code, we use algebraic data types, a popular concept in functional programming.
Either left or right
An algebraic data type is a kind of composite type (so a type which is a result of combining a few types together). Sound familiar? Yes! We have a similar construct in TypeScript, and it’s called a union type.
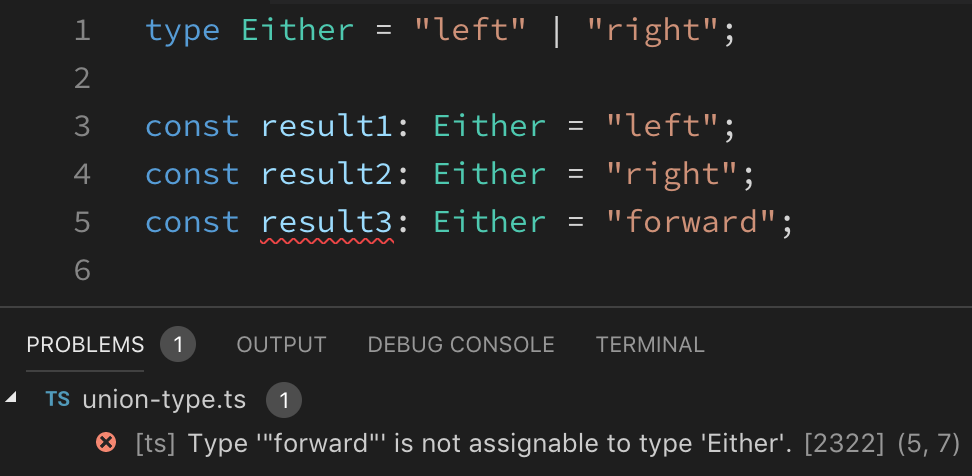
Result type accepts only “left” or “right” value, “forward” is not assignable to the type Either. Is this an algebraic data type we are looking for? Not yet, first we need an interface.
type Left = { tag: "left", error: Error };
type Right<T> = { tag: "right", result: T };
type Either<T> = Left | Right<T>;Either is now a tagged union (discriminated union). The TypeScript’s type system is structural and tagged union is as close as we can get to an algebraic data type in TypeScript. This notation is actually very close to how we can export algebraic data types to JSON in purely functional languages like Haskell.
What’s the benefit of such an approach? While it might look like unnecessary boilerplate, it pays off. We can now simulate pattern matching with a switch statement.
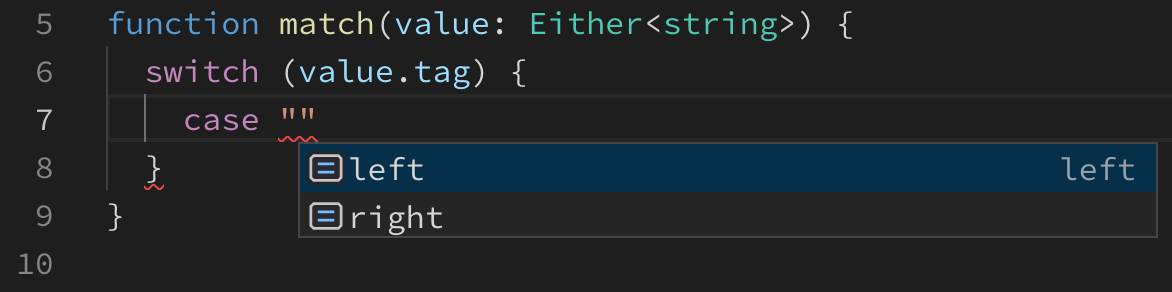
The function allows us to match on a tag of a value of type Either<string>. Right away we get a hint on all values from which we can choose.
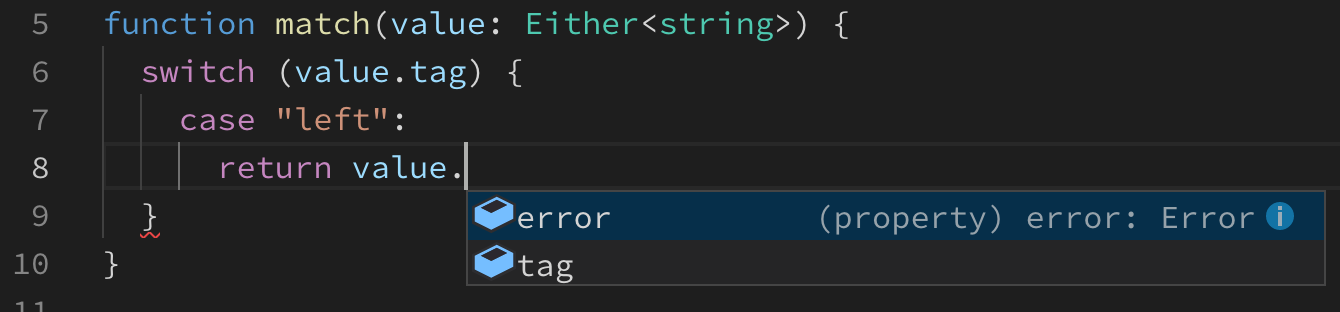
Now TypeScript knows that the only available members of the Left value are tag and error. The result is only available on the Right type which we know doesn’t fall under the tag that equals left.
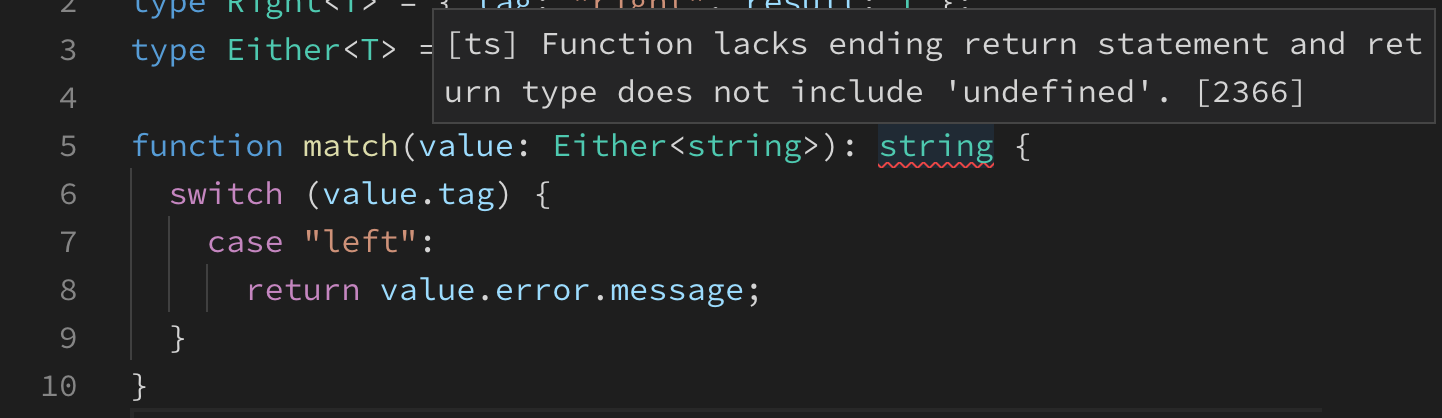
I forgot to handle the right case! Thanks to specifying the match return type explicitly, TypeScript can warn me about cases I forgot to handle.

Now, match returns a string for every case of value it accepts. Now you should have a grasp for what algebraic data types can be useful. The reusable implementation of match that generalizes better can be implemented using callbacks.
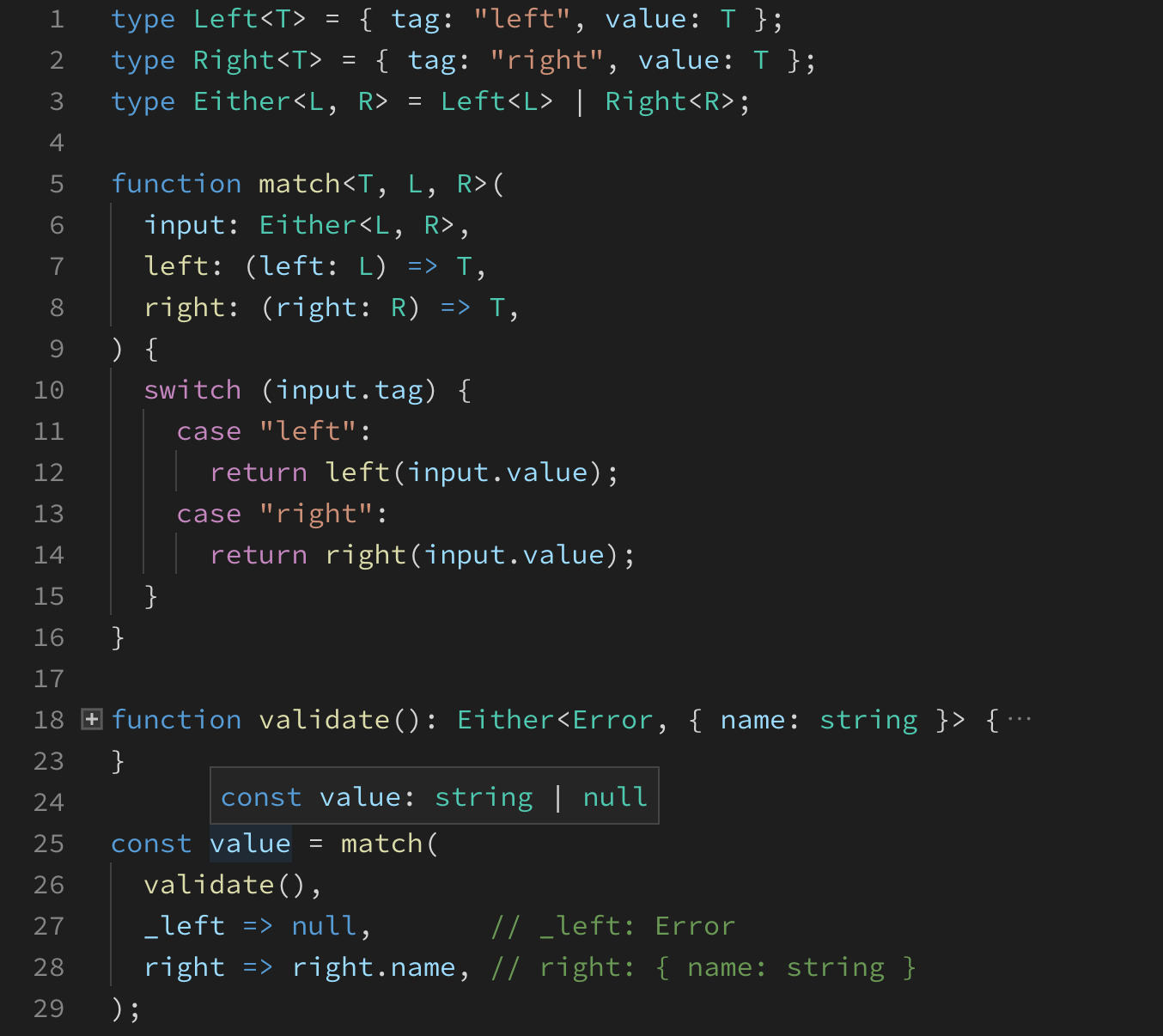
What’s really neat about this particular match implementation is that as long as you get the type of the input right, the rest of the types for a match call are inferred, and no additional typing is required.
Before we look into a more complex example, have you heard about Either type before? There’s a good chance you did!
Either type is often used when we have to handle either of two cases. By convention, Left is used to hold an error, and Right is used to hold correct (“the right“) value. If you have a problem with remembering the order and the “correct-right” analogy doesn’t stick, think about arguments we’re used to and callbacks in Node.js.
import fs from "fs";
fs.readFile("input.txt", (err, data) => {
if (err) return console.error(err);
console.log(data.toString());
});The first argument is an error (left side of the arguments list) and the second is a result (the right side of the arguments list).
If I got you interested in algebraic data types, take a look at fp-ts, a library which defines many different algebraic data types to choose from and has a rich ecosystem.
Type-safe reducers
The very same technique we used to come up with our Either type can be applied where using switch statement is already popular, in redux’s reducer. Instead of having an only binary option of Left or Right, we can have as many options as action types we have to handle. For the record, we strive to optimize for reducer correctness and ease of development thanks to accurate autocompletion.
enum ActionTypes {
REQUEST_SUCCESS = "REQUEST_SUCCESS",
REQUEST_FAILURE = "REQUEST_FAILURE",
}
type SFA<T, P> = { type: T, payload: P };
const createAction = <T extends ActionTypes, P>(
type: T,
payload: P
) : SFA<T, P> => ({ type, payload });
const success = (payload: { items: Todo[] }) =>
createAction(ActionTypes.REQUEST_SUCCESS, payload);
const failure = (payload: { reason: string }) =>
createAction(ActionTypes.REQUEST_FAILURE, payload);
const actions = { success, failure };
type Action = ReturnType<typeof actions[keyof typeof actions]>;
type Todo = { id: string };
type State = { items: Todo[] , error: string };
function reducer(state: State, action: Action): State {
switch (action.type) {
case ActionTypes.REQUEST_SUCCESS:
return { ...state, items: action.payload.items, error: "" };
case ActionTypes.REQUEST_FAILURE:
return { ...state, items: [], error: action.payload.reason };
}
return state;
}I defined action types as a string enum. SFA type stands for a standard flux action and can be overloaded together with createAction to accommodate more action shapes, but this is not the most important at the moment. The interesting part is how we built the Action type. Using ReturnType, we can obtain types of actions returned by action creators directly from the actions object.
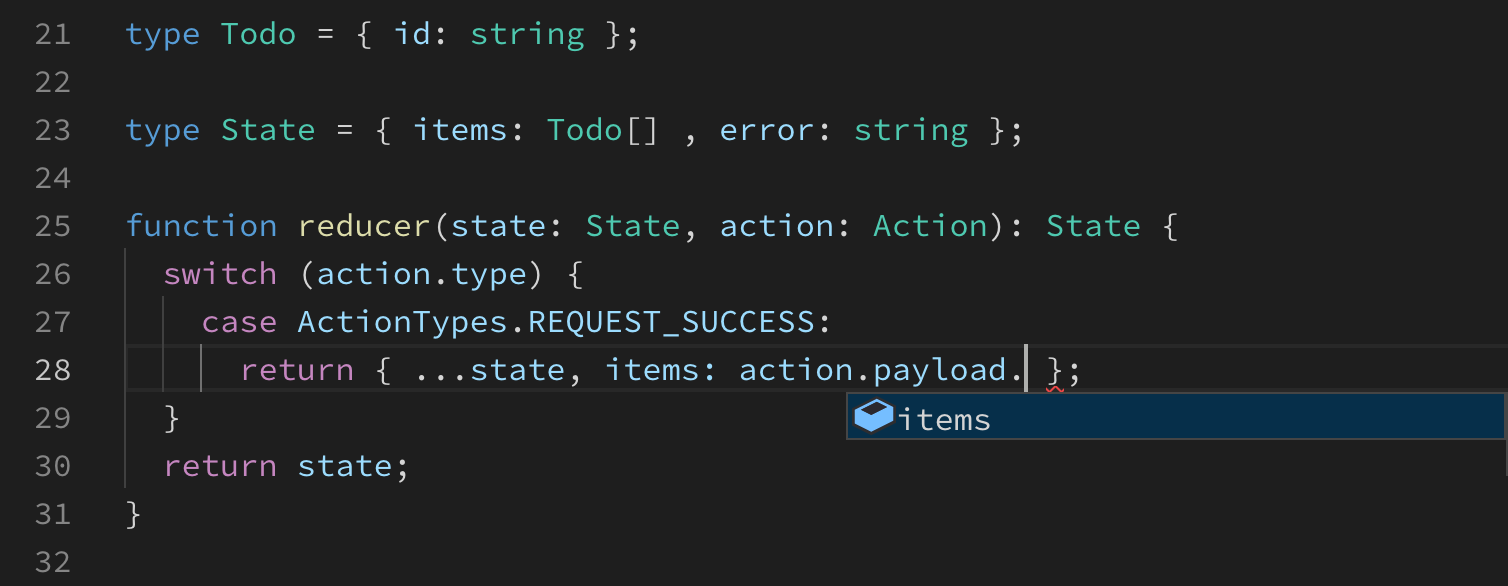
This significantly reduced the amount of typing we have to do in every reducer without compromising the type safety.
Runtime types
Have you ever defined a type for the JSON payload? In general, HTTP clients allow you to do that, but you have no guarantee that what you are actually going to fetch matches the interface you have specified. Here’s where runtime types come in. The io-ts library adopts this approach and blurs the boundary between what’s possible to type statically and what otherwise would require writing defensive code and custom type guards.
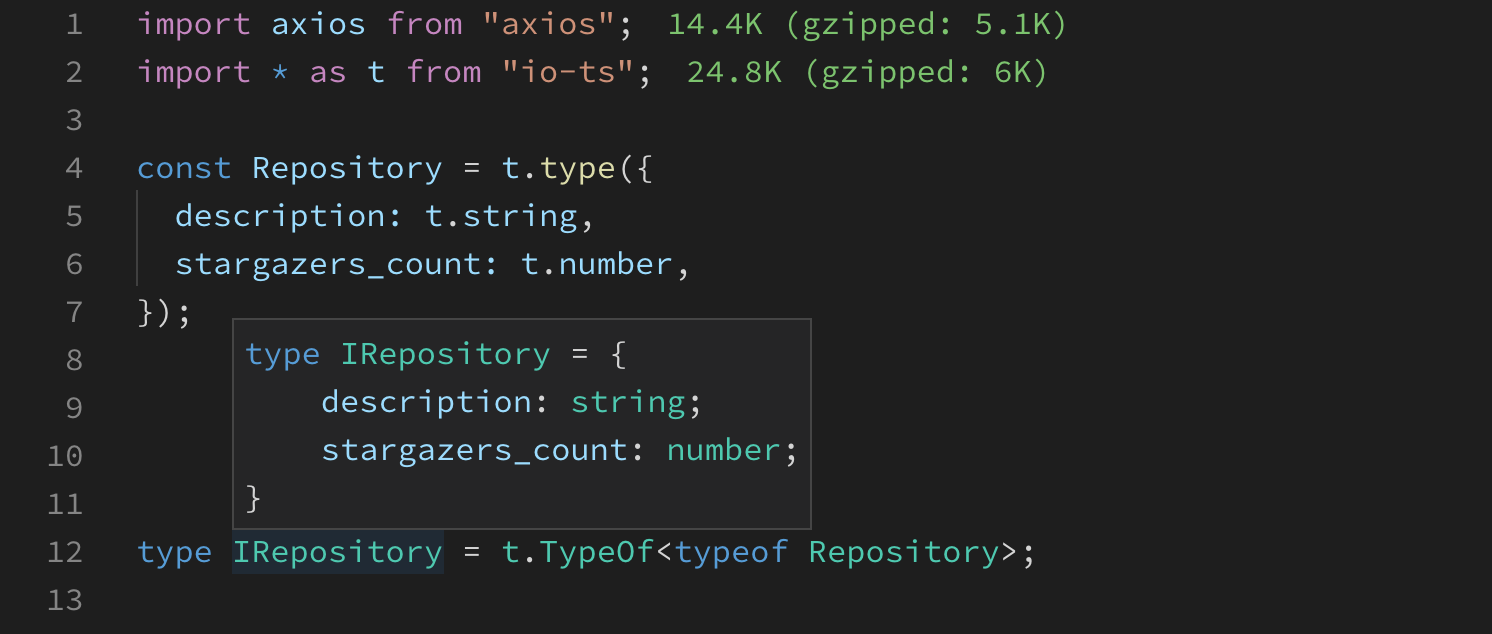
Defining Repository (runtime type) is as effortless as defining an interface in TypeScript. It’s also possible to extract the static type from the runtime type using TypeOf.
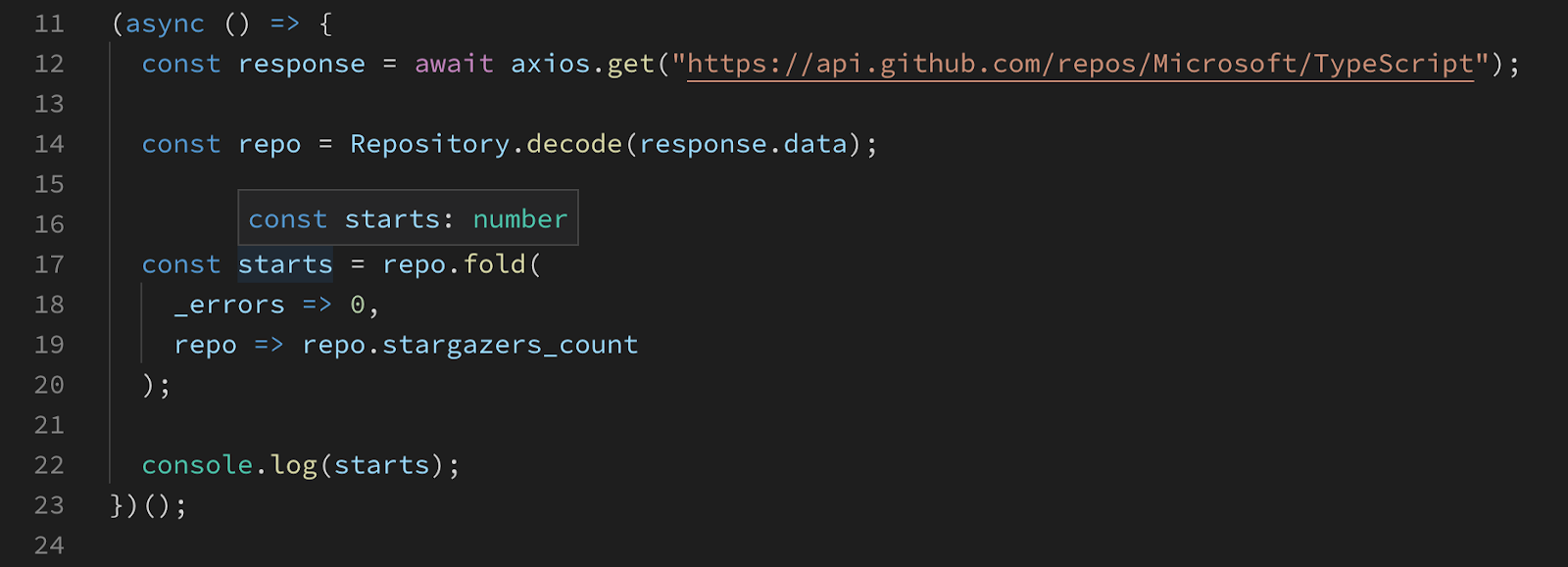
I can fetch the payload without worrying about specifying the type of the response I can’t be sure of anyway. I decode the payload to what I expect to be the Microsoft/TypeScript GitHub repository. I don’t have to define all fields, only the ones I’m interested in. Calling fold on the repo is similar to how we used the match function. In fact, the repo is of type Either which has a slightly different implementation than our Either, but the idea is the same. The left value is a list of errors that prevented payload from parsing correctly, and the right value is the repository.
Takeaways
I intentionally tried to avoid throwing and handling errors. In the provided examples errors handling is not an afterthought, we model software treating errors as part of the domain. It’s not easy but I found it to be a great learning experience.
I would also encourage you to avoid using any in your interfaces and function signatures. It’s an escape hatch that quickly propagates across all of its consumers either forcing you to lose the benefits of static typing or assert types (explicitly using “as” syntax or guard function).
I hope the provided examples give you some guideline on how you can incorporate algebraic data types into your own project. Don’t forget to try out io-ts yourself!
This article has been originaly posted on LogRocket's blog: Pattern matching and type safety in TypeScript
Photo by Fancycrave on Unsplash.
